Apprenez la cinématique inverse avec un entraînement de bras de robot

Jetons un autre coup d’œil à notre circuit et ajoutons un composant utile qui nous permettra de contrôler rapidement et facilement la valeur de notre coordonnée d’objectifs pour notre projet: un joystick! Nous pouvons utiliser l’axe supérieur du joystick pour augmenter et diminuer la valeur de notre variable Y, qui fait monter et descendre notre robot, et utiliser l’axe gauche-droite du joystick pour augmenter et diminuer la valeur de notre variable X, déplaçant notre robot de gauche à droite.

Connectez la broche de tension positive du joystick à la broche 5V sur l’Arduino, à travers les rails de puissance de la planche à pain. Connectez la broche GND au rail GND de la planche à pain et les broches X et Y du joystick aux broches A0 et A1 sur l’Arduino.

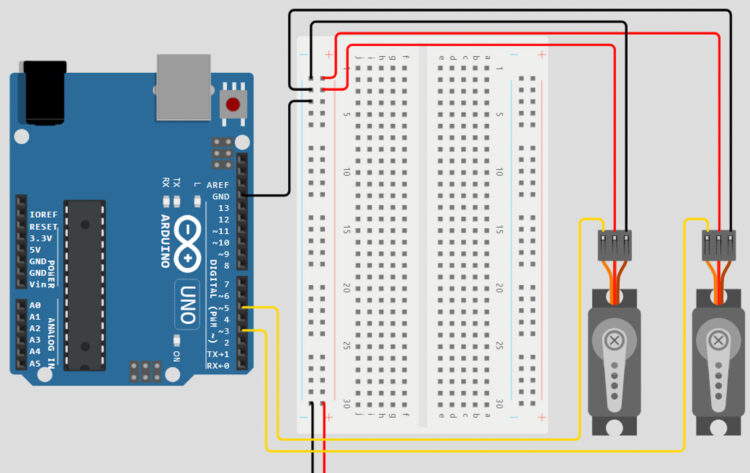
Maintenant que nous avons câblé tous les composants dont nous aurons besoin, la dernière étape sera de convertir nos équations cinématiques inverses en code et en ajoutant les quelques lignes dont nous avons besoin pour lire nos valeurs de joystick! Heureusement, les Arduinos sont excellents en mathématiques et ont des fonctions pour chacune des opérations mathématiques dont nous aurons besoin pour terminer les calculs intégrés dans le langage de programmation.

#include "Servo.h"
Servo servoOne;
Servo servoTwo;
//Setting up our IK variables
double x = 30.0;
double y = 120.0;
double linkOne = 100.0;
double linkTwo = 100.0;
double alphaOne;
double alphaTwo;
double alphaFinal;
double betaOne;
double betaTwo;
double betaFinal;
double c;
double d = 60.0;
double e;
int xval;
int yval;

void setup() {
  Serial.begin(9600);
  servoOne.attach(3);
  servoTwo.attach(5);
}

void loop()
{
  //IK Calculations
  yval = analogRead(A0);
  xval = analogRead(A1);
  c = sqrt((x*x)+(y*y));
  e = sqrt(((d-x)*(d-x))+(y*y));
  alphaOne = atan(y/x) * (180/PI);
  alphaTwo = acos(((linkTwo*linkTwo)-(c*c)-(linkOne*linkOne))
            /(-2*linkOne*c)) * (180/PI);
  betaOne = atan(y/(d-x)) * (180/PI);
  betaTwo = acos(((linkTwo*linkTwo)-(e*e)-(linkOne*linkOne))
            /(-2*linkOne*e)) * (180/PI);
  if(x < 0){ alphaFinal = 180 + ((alphaOne) + (alphaTwo)); betaFinal = 180 - ((betaOne) + (betaTwo)); } else if(x > d){
      alphaFinal = ((alphaOne) + (alphaTwo));
      betaFinal = -1 * ((betaOne) + (betaTwo));
    }
  else{
      alphaFinal = ((alphaOne) + (alphaTwo));
      betaFinal = 180 - ((betaOne) + (betaTwo));
    }

  //Printing the results! 
  Serial.print("alpha One: ");
  Serial.print(alphaOne);
  Serial.print(" beta One:");
  Serial.print(betaOne);
  Serial.print(" alpha Two: ");
  Serial.print(alphaTwo);
  Serial.print(" beta Two:");
  Serial.print(betaTwo);
  Serial.print(" Alpha: ");
  Serial.print(alphaFinal);
  Serial.print(" Beta: ");
  Serial.println(betaFinal);
  servoOne.write(alphaFinal);
  servoTwo.write(betaFinal);

/*
Depending on your customization, it may be a good idea to add some limits here! If you see your arms acting squirrely, add a statement  such as “if(xVal > 800 && xVal < 200)” */ if(xval > 800){
    x-=5;
  }
  if(xval < 300){ x+=5; } if(yval > 800){
    y-=5;
  }
  if(yval < 300){
    y+=5;
  }
}

Décomposons le code que nous venons d’envoyer à notre Arduino. L’une des premières choses que notre code accomplit est de créer des variables pour notre position d’objectif sur notre grille sous la forme d’un ensemble de x et y coordonnées. Dans ce cas, les coordonnées (30, 120) ont été choisies de sorte que le robot commence au centre de la grille. Ces valeurs peuvent être modifiées pour que le stylo commence n’importe où sur la grille que vous souhaitez! Ensuite, nous pouvons créer le reste des variables dont nous avons besoin pour nos calculs. Chaque étape des équations a sa propre variable dans le code.

Les variables linkone et linktwo représentent les longueurs des liens de notre système, qui sont à la fois 100 mm. Ensuite, les variables alphaone, alphatwo, alphafinal, betaone, betatwoet bétafinal représentent toutes nos variables sous-angle et d’angle final. Enfin, le c et e Les variables sont nos lignes de triangle théorique, et d représente la distance entre les arbres de nos deux actionneurs.

Maintenant que nous avons toutes les variables nécessaires, nous pouvons commencer à convertir nos équations à la clématisation inverse en code. Bien que ces lignes de code puissent sembler beaucoup plus compliquées que certaines de nos lignes de code précédentes, si vous les passez étape par étape, vous verrez que nous prenons chaque action que nous avons développée dans nos équations et la convertissant en code que notre Arduino peut comprendre.

Une fois que nous avons des valeurs pour toutes nos variables et que nous avons terminé nos principaux calculs, il ne reste plus que de combiner nos variables de sous-angle en variables d’angle final qui seront envoyées à nos actionneurs. Comme vous vous en souvenez peut-être de nos calculs précédents, certains de nos calculs d’angle final dépendent de la valeur de notre x variable. Heureusement, trois ensembles d’instructions conditionnelles sont tout ce dont nous avons besoin pour nous assurer que nos angles sont calculés correctement, quoi qu’il arrive x et y les valeurs sont choisies.