Alphageométrie: un système d’IA au niveau de l’Olympiade pour la géométrie

Recherche
Notre système d’IA dépasse l’approche de pointe pour les problèmes de géométrie, avançant le raisonnement d’IA en mathématiques
Reflétant l’esprit olympique de la Grèce antique, L’Olympiade mathématique internationale est une arène moderne pour les mathématiciens du lycée les plus brillants du monde. La compétition présente non seulement des jeunes talents, mais est devenue un terrain de test pour les systèmes d’IA avancés en mathématiques et en raisonnement.
Dans un article publié aujourd’hui dans Naturenous introduisons l’alphageométrie, un système d’IA qui résout des problèmes de géométrie complexes à un niveau approchant d’une olympiade humaine-médaliste or – une percée dans la performance de l’IA. Dans un test d’analyse comparative de 30 problèmes de géométrie des Olympiades, l’alphageométrie a résolu 25 dans le délai standard de l’Olympiade. À titre de comparaison, le système de pointe précédent a résolu 10 de ces problèmes de géométrie, et le médaillé d’or humain moyen a résolu 25,9 problèmes.
Dans notre ensemble d’analyses comparatives de 30 problèmes de géométrie des olympiades (IMO-AG-30), compilés à partir des Olympiades de 2000 à 2022, l’alphageométrie a résolu 25 problèmes sous les délais de compétition. Cela aborde le score moyen des médaillés d’or humains sur ces mêmes problèmes. L’approche précédente de pointe, connue sous le nom de «méthode de Wu», a résolu 10.
Les systèmes d’IA luttent souvent avec des problèmes complexes en géométrie et en mathématiques en raison d’un manque de compétences de raisonnement et de données de formation. Le système d’alphageométrie combine le pouvoir prédictif d’un modèle de langue neuronale avec un moteur de déduction lié aux règles, qui fonctionne en tandem pour trouver des solutions. Et en développant une méthode pour générer un vaste pool de données d’entraînement synthétiques – 100 millions d’exemples uniques – nous pouvons entraîner l’alphageométrie sans aucune démonstration humaine, évitant le goulot d’étranglement des données.
Avec l’alphageométrie, nous démontrons la capacité croissante de l’IA à raisonner logiquement et à découvrir et à vérifier de nouvelles connaissances. La résolution de problèmes de géométrie au niveau de l’Olympiade est une étape importante dans le développement d’un raisonnement mathématique profond sur la voie des systèmes d’IA plus avancés et généraux. Nous sommes ouverts le Code et modèle d’alphageométrieet espérons que, avec d’autres outils et approches dans la génération et la formation de données synthétiques, cela aide à ouvrir de nouvelles possibilités à travers les mathématiques, les sciences et l’IA.
«
Cela est parfaitement logique pour moi maintenant que les chercheurs de l’IA essaient d’abord leur main sur les problèmes de géométrie de l’OMI, car trouver des solutions pour eux fonctionne un peu comme les échecs dans le sens où nous avons un nombre assez petit de mouvements sensés à chaque étape. Mais je trouve toujours étonnant qu’ils puissent le faire fonctionner. C’est une réalisation impressionnante.
Ngô Bảo Châu, médaillé des champs et médaillé d’or OMI
L’alphageométrie adopte une approche neuro-symbolique
L’alphageométrie est un système neuro-symbolique composé d’un modèle de langage neuronal et d’un moteur de déduction symbolique, qui travaillent ensemble pour trouver des preuves pour les théorèmes de géométrie complexes. Semblable à l’idée de «Penser, rapide et lent», Un système fournit des idées rapides et« intuitives », et l’autre prise de décision plus délibérée et rationnelle.
Étant donné que les modèles de langage excellent dans l’identification des modèles généraux et des relations dans les données, ils peuvent rapidement prédire des constructions potentiellement utiles, mais n’ont souvent pas la capacité de raisonner rigoureusement ou d’expliquer leurs décisions. Les moteurs de déduction symboliques, en revanche, sont basés sur la logique formelle et utilisent des règles claires pour arriver à des conclusions. Ils sont rationnels et explicables, mais ils peuvent être «lents» et inflexibles – en particulier lorsqu’ils traitent de grands problèmes complexes par eux-mêmes.
Le modèle de langue de l’alphageométrie guide son moteur de déduction symbolique vers des solutions probables aux problèmes de géométrie. Les problèmes de géométrie des olympiades sont basés sur des diagrammes qui ont besoin d’ajouter de nouvelles constructions géométriques avant de pouvoir être résolues, telles que des points, des lignes ou des cercles. Le modèle de langue de l’alphageométrie prédit quelles nouvelles constructions seraient les plus utiles à ajouter, à partir d’un nombre infini de possibilités. Ces indices aident à combler les lacunes et permettent au moteur symbolique de faire d’autres déductions sur le diagramme et de se rapprocher de la solution.
Alphageométrie résolvant un problème simple: étant donné le diagramme de problèmes et ses prémisses de théorème (à gauche), l’alphageométrie (milieu) utilise d’abord son moteur symbolique pour déduire de nouvelles instructions sur le diagramme jusqu’à ce que la solution soit trouvée ou que de nouvelles instructions soient épuisées. Si aucune solution n’est trouvée, le modèle de langue de l’alphageométrie ajoute une construction potentiellement utile (bleu), ouvrant de nouveaux chemins de déduction pour le moteur symbolique. Cette boucle continue jusqu’à ce qu’une solution soit trouvée (à droite). Dans cet exemple, une seule construction est requise.
Alphageométrie résolvant un problème d’Olympiad: Problème 3 de l’Olympiade internationale de mathématiques (gauche) et une version condensée de la solution de l’alphageométrie (à droite). Les éléments bleus sont des constructions ajoutées. La solution de l’alphageométrie a 109 étapes logiques.
Générer 100 millions d’exemples de données synthétiques
La géométrie repose sur la compréhension de l’espace, de la distance, de la forme et des positions relatives, et est fondamental pour l’art, l’architecture, l’ingénierie et de nombreux autres domaines. Les humains peuvent apprendre la géométrie en utilisant un stylo et un papier, examiner les diagrammes et utiliser les connaissances existantes pour découvrir de nouvelles propriétés et relations géométriques plus sophistiquées. Notre approche de génération de données synthétiques émule ce processus de renforcement des connaissances à grande échelle, nous permettant de former l’alphageométrie à partir de zéro, sans aucune démonstration humaine.
En utilisant un calcul hautement parallélisé, le système a commencé par générer un milliard de diagrammes aléatoires d’objets géométriques et a dérivé de manière exhaustive toutes les relations entre les points et les lignes de chaque diagramme. L’alphageométrie a trouvé toutes les preuves contenues dans chaque diagramme, puis a travaillé en arrière pour savoir quelles constructions supplémentaires, le cas échéant, étaient nécessaires pour arriver à ces preuves. Nous appelons ce processus «déduction symbolique et trace».
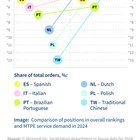
Représentations visuelles des données synthétiques générées par alphageométrie
Cet énorme pool de données a été filtré pour exclure des exemples similaires, résultant en un ensemble de données de formation final de 100 millions d’exemples uniques de difficulté variable, dont neuf millions comportaient des constructions supplémentaires. Avec autant d’exemples de la façon dont ces constructions ont conduit à des preuves, le modèle de langue de l’alphageométrie est capable de faire de bonnes suggestions pour de nouvelles constructions lorsqu’ils sont présentés avec des problèmes de géométrie olympiale.
Raisonnement mathématique pionnier avec l’IA
La solution à chaque problème de l’Olympiad fournie par l’alphageométrie a été vérifiée et vérifiée par ordinateur. Nous avons également comparé ses résultats avec les méthodes d’IA précédentes et les performances humaines à l’Olympiade. De plus, Evan Chen, entraîneur de mathématiques et ancienne médaillée d’or de l’Olympiade, a évalué une sélection de solutions d’alphageométrie pour nous.
Chen a déclaré: «La sortie de l’alphageométrie est impressionnante car elle est à la fois vérifiable et propre. Les solutions d’IA passées aux problèmes de concurrence basées sur la preuve ont parfois été à succès (les sorties ne sont que parfois correctes et ont besoin de contrôles humains). L’alphageométrie n’a pas cette faiblesse: ses solutions ont une structure veillante à la machine. Pourtant, malgré cela, sa production est toujours lisible par l’homme. On aurait pu imaginer un programme informatique qui a résolu les problèmes de géométrie par des systèmes de coordonnées par force brute: pensez aux pages et aux pages du calcul de l’algèbre fastidieux. L’alphageométrie n’est pas ça. Il utilise des règles de géométrie classique avec des angles et des triangles similaires comme les élèves. »
«
La sortie de l’alphageométrie est impressionnante car elle est à la fois vérifiable et propre… il utilise des règles de géométrie classique avec des angles et des triangles similaires comme les étudiants.
Evan Chen, entraîneur de mathématiques et médaillée d’or olympiale
Comme chaque Olympiade présente six problèmes, dont seulement deux sont généralement axés sur la géométrie, l’alphageométrie ne peut être appliquée qu’à un tiers des problèmes lors d’une Olympiade donnée. Néanmoins, sa capacité de géométrie en fait à elle seule le premier modèle d’IA au monde capable de passer le seuil de médaille de bronze de l’OMI en 2000 et 2015.
En géométrie, notre système aborde la norme d’un médaliste or IMO, mais nous avons un œil sur un prix encore plus grand: le raisonnement avancé pour les systèmes d’IA de nouvelle génération. Étant donné le potentiel plus large de la formation des systèmes d’IA à partir de zéro avec des données synthétiques à grande échelle, cette approche pourrait façonner la façon dont les systèmes d’IA du futur découvrent de nouvelles connaissances, en mathématiques et au-delà.
L’alphageométrie s’appuie sur Google Deepmind et le travail de Google Research pour pionnier du raisonnement mathématique avec l’IA – de Explorer la beauté des mathématiques pures à Résoudre des problèmes mathématiques et scientifiques avec les modèles de langues. Et plus récemment, nous avons introduit Funsearchce qui a fait les premières découvertes dans les problèmes ouverts en sciences mathématiques à l’aide de modèles de langues importants.
Notre objectif à long terme reste de construire des systèmes d’IA qui peuvent généraliser à travers les domaines mathématiques, en développant la résolution de problèmes et le raisonnement sophistiqués sur lesquels les systèmes d’IA généraux dépendront, tout en étendant les frontières des connaissances humaines.
Remerciements
Ce projet est une collaboration entre l’équipe Google Deepmind et le département informatique de l’Université de New York. Les auteurs de ce travail incluent Trieu Trinh, Yuhuai Wu, Quoc Le, He He et Thang Luong. Nous remercions Rif A. Saurous, Denny Zhou, Christian Szegedy, Delesley Hutchins, Thomas Kipf, Hieu Pham, Petar Veličković pour leur aide et leur soutien. Nous tenons également à remercier Google Deepmind Leadership pour le soutien, en particulier Ed Chi, Koray Kavukcuoglu, Pushmeet Kohli et Demis Hassabis.