Day22 / 200 🔄 Une introduction à la traduction d’images et à la rotation dans la vision par ordinateur! | par Adityajani | Août 2025

Appuyez sur Entrée ou cliquez pour afficher l’image en taille réelle

Bonjour encore, visionnaires! 👋

Aujourd’hui, nous plongeons dans le transformations fondamentales qui nous permettent de manipuler la position et l’orientation des images: traduction et rotation. Ce sont le fondement de nombreuses tâches de vision par ordinateur, de l’alignement des images à la reconnaissance des objets de différents points de vue. Explorons la théorie derrière ces opérations fondamentales mais puissantes.

Avant de zoomer sur la traduction et la rotation, comprenons ce transformations géométriques sont. Essentiellement, ce sont des opérations qui Carte les coordonnées des pixels dans une image d’entrée vers de nouvelles coordonnées dans une image de sortie. Cette cartographie détermine comment l’image est transformée géométriquement.

• 🔄 Traduction – images en mouvement dans l’espace 2D
• 🌀 Rotation – Transformer les images autour d’un point
• 📏 Éclatement – redimensionner les images vers le haut ou vers le bas
• 🪞 Réflexion – Images en miroir
• 📐 Tonte – Images inclinées

Aujourd’hui, nous nous concentrerons sur le deux premiers fondamentaux! 🎯

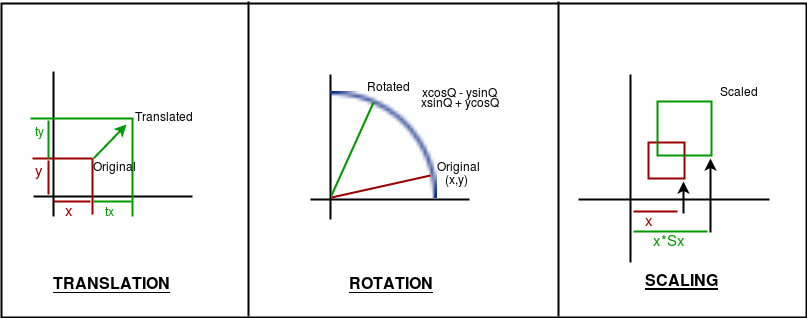
Traduction d’image est le processus de déplacement d’une image d’un endroit à un autre dans un plan 2D. Considérez-le comme glissant une photographie sur une table. Chaque pixel de l’image d’origine est décalé par le Même quantité dans les directions horizontales (x) et verticales (y).

Disons que nous avons un pixel aux coordonnées (x, y) dans l’image d’origine. Après la traduction par un décalage horizontal de tₓ et un décalage vertical de tᵧles nouvelles coordonnées (x ‘, y’) de ce pixel sera:

x' = x + tₓ
y' = y + tᵧ

• ➡️ Tₓ positif déplacera l’image vers le droite
• ⬅️ Tₓ négatif déplacera l’image vers le gauche
• ⬇️ Tᵧ positif déplacera l’image vers le bas
• ⬆️ Tᵧ négatif déplacera l’image vers le haut

Nous pouvons représenter cette traduction mathématiquement en utilisant un Matrice de transformation 3 × 3 dans les coordonnées homogènes. Cela nous permet d’effectuer des transformations affines (comme la traduction) en utilisant la multiplication matricielle. Un point (x, y) est représenté comme un vecteur (x, y, 1) ᵀ.

Le matrice de traduction t est donné par:

T = (1  0  tₓ)
(0  1  tᵧ)
(0  0   1)

Appliquer cette matrice à notre point (x, y):

(x')   (1  0  tₓ) (x)   (x + tₓ)
(y') = (0  1  tᵧ) (y) = (y + tᵧ)
(1 )   (0  0   1) (1)   (  1   )

Cette multiplication matricielle confirme nos équations de transformation de coordonnées antérieures! ✅

Rotation d’image implique de tourner une image autour d’un point spécifique, généralement le Origine (0, 0) ou le centre de l’image. La rotation est définie par un angle θqui est généralement mesuré en degrés ou en radians. Un angle positif indique généralement un rotation dans le sens inverse.

Considérer un pixel à (x, y) que nous voulons tourner sous un angle θ dans le sens antihoraire autour de l’origine. Les nouvelles coordonnées (x ‘, y’) sont donnés par:

x' = x cos θ - y sin θ
y' = x sin θ + y cos θ

Semblable à la traduction, nous pouvons représenter la rotation en utilisant un Matrice de rotation 3 × 3 R Dans les coordonnées homogènes:

R = (cos θ  -sin θ   0)
(sin θ   cos θ   0)
(  0       0     1)

Appliquer cette matrice à notre point (x, y):

(x')   (cos θ  -sin θ   0) (x)   (x cos θ - y sin θ)
(y') = (sin θ   cos θ   0) (y) = (x sin θ + y cos θ)
(1 )   (  0       0     1) (1)   (        1        )

Souvent, nous voulons Faites pivoter une image autour de son centre (cₓ, cᵧ) plutôt que l’origine. Pour ce faire, nous effectuons une séquence de Trois transformations:

1. 🎯 Traduire: Déplacer l’image pour le centre (cₓ, cᵧ) est à l’origine
2. 🌀 Rotation: Effectuer la rotation par θ Autour de l’origine
3. 🔙 Traduire à nouveau: Passez l’image à sa position d’origine

Le Matrice de transformation combinée est le produit de ces matrices individuelles: T_final = t₂ × r × t₁ 🎯

Lors de la mise en œuvre de ces transformations, il y a Deux approches principales:

• Processus: Itérer dans chaque pixel d’entrée, calculer ses nouvelles coordonnées et la placer dans l’image de sortie
• Défi: Cela peut conduire à lacunes ou pixels qui se chevauchent dans l’image de sortie ❌

• Processus: Itérer à travers chaque emplacement de pixel de sortie, calculer le pixel d’entrée qui lui correspond à l’aide de la transformation inverse et copier la valeur
• Avantage: Cela garantit Chaque pixel de la sortie est rempliéviter les lacunes et produire de meilleurs résultats ✅

Pour une rotation de θl’inverse est simplement une rotation de -θ. Les équations inverses sont:

x = x' cos θ + y' sin θ
y = -x' sin θ + y' cos θ

La traduction et la rotation sont fondamental pour de nombreuses applications:

Enregistrement de plusieurs images de la même scène, cruciale pour:

• 📷 Création de panorama à partir de plusieurs plans
• 🛰️ Imagerie satellite Analyse à travers le temps
• 🏥 Balayage médical Enregistrement du diagnostic

Systèmes de construction qui sont invariant à la position et à l’orientation d’un objetutilisé dans:

• 🚗 Véhicules autonomes Pour la détection des panneaux de route
• 🏭 Contrôle de qualité Systèmes de fabrication
• 📱 Applications mobiles pour la reconnaissance des produits

Combiner plusieurs images en une seule vue panoramique pour:

• 🌄 Photos de paysage avec de superbes vues
• 🏢 Visites virtuelles à 360 degrés des bâtiments
• 🔬 Microscopie pour une grande imagerie de champ

Créer plus de données de formation En traduisant et en tournant les images existantes en:

• 🧠 Améliorer la robustesse des modèles d’apprentissage automatique
• 📊 Développer des ensembles de données sans collecter de nouvelles données
• 🎯 Améliorer les performances du modèle à travers différentes orientations

• Utiliser interpolation bicubique Pour les résultats plus lisses
• Appliquer anti-aliasing Pour réduire les bords de déchaînement
• Considérer précision des sous-pixels pour des transformations précises

• Valeurs trigonométriques de pré-comparer (sin θ, cos θ) pour l’efficacité
• Considérer Accélération du GPU pour les opérations à grande échelle
• Utiliser tables de recherche pour les transformations répétées

• Poignée Coordonnées hors limites gracieusement
• Considérer Stratégies de rembourrage Pour éviter les artefacts aux frontières d’image
• Mettre en œuvre Conditions aux limites appropriées Pour différents cas d’utilisation

Traduction d’image et rotation sont les blocs de construction de base pour manipuler la disposition spatiale des pixels. Comprendre le sous-jacent principes mathématiques et représentations matricielles est crucial pour quiconque s’aventure dans la vision par ordinateur, car ces concepts constituent le fondement des tâches plus complexes et un large éventail d’applications puissantes.

• ✅ Traduction déplace des images en utilisant un ajout simple
• ✅ Rotation tourne des images à l’aide de fonctions trigonométriques
• ✅ Représentations matricielles Dans les coordonnées homogènes, permettent un calcul efficace
• ✅ Cartographie inverse est la méthode préférée pour les résultats de haute qualité
• ✅ Les applications sont vastesde la photographie aux systèmes autonomes