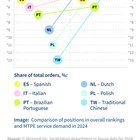
(R) Processus gaussien pour approximer la dynamique des véhicules
|
Il y a quelque temps, je travaillais sur la localisation avec le GPS et je pensais: pourrions-nous coder la dynamique des véhicules directement dans le noyau GP? Je sais que les GP sont utilisés pour modéliser les paramètres dans les modèles physiques. Mais mon idée était que la trajectoire d’une voiture ressemble à un échantillon de GP lisse. Une voiture plus rapide prend des chemins plus lisses, tout comme les échelles de longueur plus longues produisent un GPS plus fluide. Au lieu de modélisation
Les deux utilisent un noyau RBF. Nous maximisons donc essentiellement la fonction de probabilité: Qui se traduit par quelque chose comme « Compte tenu de la vitesse, à quel point est-il probable que ces points de données proviennent de ce véhicule? » L’algorithme se passe comme ceci:
J’ai adapté l’échelle de longueur du noyau Avec le noyau optimisé en main, vous pouvez poser des questions comme: «Compte tenu de cette course et d’une vitesse, ma voiture peut-elle la suivre?" Comme le GP est un modèle probabiliste, il ne donne pas de réponse binaire que nous avons demandée. Nous pourrions optimiser pour «la vitesse la plus probable» de la même manière que nous avons optimisé les échelles de longueur. Cependant, cela ressemblerait davantage à demander: «Quelle est la vitesse la plus probable que cette course peut être réalisée?», Ce qui est acceptable pour garder votre Tesla sur la route, mais pas optimale pour la course. Mon approche était de définir une tolérance acceptable pour l’écart par rapport à la racine. Avec ces contraintes en main, je gère une optimisation basée sur une fenêtre heuristique pour une raceline donnée: https://i.redd.it/e7qteia2s9ef1.gif Résultats? Les temps de plan LAP exécutés par le simulateur étaient proches des tours de l’homme. Le modèle ne tenait pas compte des limites d’accélération, de sorte que les performances réelles ont légèrement échoué au plan prévu, mais je pense que cela a prouvé le concept. Il y a beaucoup de choses qui pourraient être améliorées dans le modèle. L’une des plus grandes limites est les modèles indépendants des coordonnées X et Y. Certaines des choses que j’ai aussi essayées:
Voici le code et les données si vous souhaitez l’améliorer: soumis par / U / Northafternoon4930 |