La nouvelle percée d’Alphaevolve: s’attaquer au problème des baisers et repousser les limites des mathématiques | par Hiya Chatterjee | Mai 2025

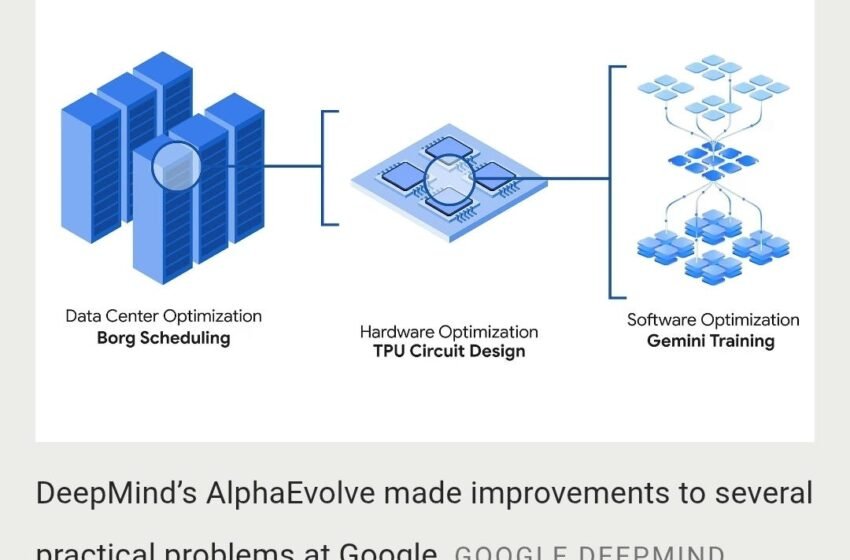
Dans un saut audacieux pour l’intelligence artificielle et les mathématiques pures, un nouveau modèle d’IA nommé Alphaevolve a fait la une des journaux en offrant de nouvelles informations sur une énigme séculaire connue sous le nom de problème de baisers, tout en générant simultanément des optimisations pratiques dans la géométrie, la théorie des nombres et les optimisations à plus grande dimension.

Développé par une équipe de recherche collaborative fusionnant les esprits de l’apprentissage en profondeur, de la physique théorique et des mathématiques informatiques, Alphaevolve représente une nouvelle race d’IA – non seulement du contenu de la résolution de problèmes, mais de découvrir de nouvelles frontières dans la façon dont nous comprenons la structure de l’espace lui-même.

—

Le problème des baisers est une question géométrique trompeusement simple: quel est le nombre maximal de sphères d’unité non chevauchantes qui peuvent toucher simultanément (ou «baiser») une autre sphère d’unité centrale?

En trois dimensions, la réponse est de 12 – un fait a d’abord réfléchi par Isaac Newton et officiellement prouvé au 20e siècle. Cependant, à mesure que les dimensions augmentent, le problème devient exponentiellement plus complexe. Par exemple, en huit et vingt-quatre dimensions, les solutions reposent respectivement sur des réseaux mathématiques hautement spécialisés comme le réseau E8 et Leech.

Malgré les progrès de ces dimensions particulières, les mathématiciens ont longtemps eu du mal à généraliser la solution ou à trouver des limites supérieures pour des dimensions arbitraires. C’est là qu’Alphaevolve est intervenu.

—

Alphaevolve a été formé sur un ensemble de données multimodal combinant des entrées géométriques, topologiques et numériques des articles de recherche historiques, des données de simulation et des structures algébriques abstraites. Au lieu d’être invité à «résoudre» le problème des baisers, il a été demandé de générer des conjectures, de tester des stratégies d’optimisation et d’identifier des modèles inexplorés.

Voici où cela devient fascinant: Alphaevolve n’a pas abordé le problème grâce à des simulations de force brute. Il a exploité la manipulation symbolique guidée par le renforcement et l’extraction des caractéristiques topologiques pour identifier des symétries précédemment inconnues et des structures d’emballage exceptionnelles dans des dimensions au-delà de 24.

En particulier, il a proposé une nouvelle structure de réseau heuristique pour la dimension 28 qui non seulement améliore les limites connues précédentes, mais introduit également une nouvelle symétrie non observée dans aucun réseau existant. Cette structure a ensuite été vérifiée par des mathématiciens humains et est désormais sous revue par les pairs.

—

Alors que son travail sur le problème des baisers a fait la une des journaux, Alphaevolve ne s’est pas arrêté là. Ses contributions plus larges révèlent une vision ambitieuse pour étendre les frontières de l’optimisation mathématique et de la modélisation théorique:

Alphaevolve Configurations d’emballage serrées construites dans des dimensions précédemment considérées comme intraitables en calcul. Sa capacité à simuler et à tailler des milliards d’arrangements lui a permis de faire de nouvelles estimations de densité dans plus de 30 dimensions, ouvrant des voies fraîches dans la cryptographie et les codes de correction des erreurs.

Dans les géométries hyperboliques et sphériques, Alphaevolve a découvert des modèles de carrelage et de compactification qui pourraient avoir des implications pour la cosmologie et la gravité quantique. Les chercheurs ont noté sa capacité à trouver des surfaces minimales et des flux géodésiques dans l’espace incurvé beaucoup plus efficacement que les méthodes variationnelles traditionnelles.

Alphaevolve a introduit un nouveau cadre qu’il a appelé «réduction de la symétrie consciente des contraintes», lui permettant de résoudre des problèmes d’optimisation combinatoire avec moins d’étapes de manière exponentielle que les solveurs de pointe. Cela a déjà été prometteur dans des champs allant de la logistique au repliement des protéines.

Le modèle a généré avec succès et a prouvé plus de 40 nouveaux théorèmes, dont beaucoup sont désormais formalisés pour publication. Fait intéressant, plusieurs de ces théorèmes relient la géométrie discrète à la théorie des nombres – un domaine de fusion que peu de chercheurs ont profondément exploré.

—

Les mathématiques ont toujours été une entreprise profondément humaine – la poursuite du motif, de la structure et du sens du tissu abstrait des nombres et de l’espace. Mais Alphaevolve suggère une nouvelle ère: celle où les machines ne résolvent pas seulement les problèmes mathématiques – ils collaborent à l’acte de découverte elle-même.

Les implications sont profondes. De l’avancement de la cryptographie à un meilleur emballage de sphères, à l’offre de nouveaux outils en physique via la modélisation topologique, et même à proposer des utilisations éducatives où elle peut guider les étudiants à travers des sauts conceptuels – Alphaevolve est plus qu’une expérience. C’est un partenaire dans l’évolution intellectuelle.

—

Bien que l’excitation soit élevée, la communauté mathématique équilibre l’enthousiasme avec le contrôle. Chaque résultat d’Alphaevolve subit une vérification humaine rigoureuse et des techniques de preuve formelle. Comme l’a dit un mathématicien, «il ne s’agit pas de faire confiance à l’IA. Il s’agit de le laisser nous montrer où chercher.»

Il y a aussi un débat en cours sur l’interprétabilité. Alphaevolve trouve souvent des résultats qu’il ne peut pas facilement expliquer en langage naturel, et déchiffrer le «pourquoi» derrière ses percées reste un domaine de recherche actif.

—

Alphaevolve fait allusion à un avenir où l’IA devient un collaborateur non seulement dans la science et l’ingénierie, mais la compréhension fondamentale de notre univers. Si nous pouvons enseigner aux machines à reconnaître la beauté, la symétrie et la logique comme les humains – ou même au-delà – alors les mathématiques pourraient simplement entrer dans son siècle le plus créatif à ce jour.

Pour l’instant, le problème des baisers a trouvé un nouveau compagnon – pas un mathématicien solitaire perdu dans ses pensées, mais un réseau de neurones formé sur des siècles de perspicacité humaine, rêvant dans le langage des dimensions.

—

Suivez pour plus de mises à jour sur l’IA et les mathématiques à la frontière de la découverte.

—