(R) Prévision de tirs zéro des systèmes chaotiques (ICLR 2025)
- Intelligence Artificielle
Noesis News- 0
- 4 minutes de lecture
|
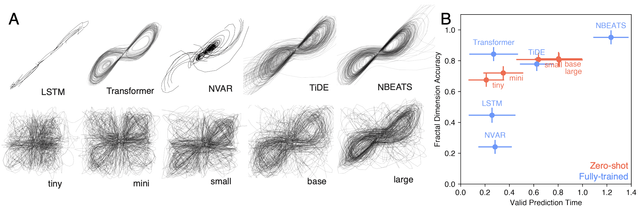
Les prévisions de séries chronologiques sont un problème difficile qui nécessite traditionnellement des modèles spécialisés formés sur mesure pour la tâche spécifique à accomplir. Récemment, inspiré par le succès des modèles de grandes langues, les modèles de fondation pré-formés sur de grandes quantités de données de séries chronologiques de divers domaines sont devenues un candidat prometteur pour les prévisions de séries chronologiques à usage général. La caractéristique déterminante de ces modèles de fondation est leur capacité à effectuer un apprentissage zéro-shot, c’est-à-dire en prévoyant un nouveau système à partir de données contextuelles limitées sans relance explicite ni réglage fin. Ici, nous évaluons si le paradigme d’apprentissage à tirs zéro s’étend à la tâche difficile de prévoir les systèmes chaotiques. Dans 135 systèmes dynamiques chaotiques distincts et 108 points de calendrier, nous constatons que les modèles de fondation produisent des prévisions compétitives par rapport aux modèles formés sur mesure (y compris les NBEAT, la marée, etc.), en particulier lorsque les données de formation sont limitées. Fait intéressant, même après l’échec des prévisions de points, les grands modèles de fondation sont capables de préserver les propriétés géométriques et statistiques des attracteurs chaotiques. Nous attribuons ce succès à la capacité des modèles de fondation à effectuer un apprentissage dans le contexte et à identifier le perroquet de contexte comme un mécanisme simple utilisé par ces modèles pour capturer le comportement à long terme des systèmes dynamiques chaotiques. Nos résultats mettent en évidence le potentiel des modèles de fondation comme outil pour sonder les systèmes non linéaires et complexes. Papier: Code: soumis par / u / wil3 |
