Ligne de journal VS Transformation du journal dans R – La différence qui induit en erreur votre analyse des données

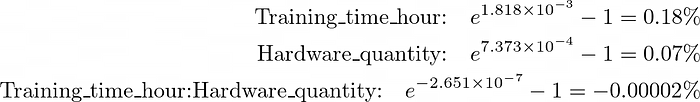
Auteur (s): Ngoc Doan

Publié à l’origine sur Vers l’IA.

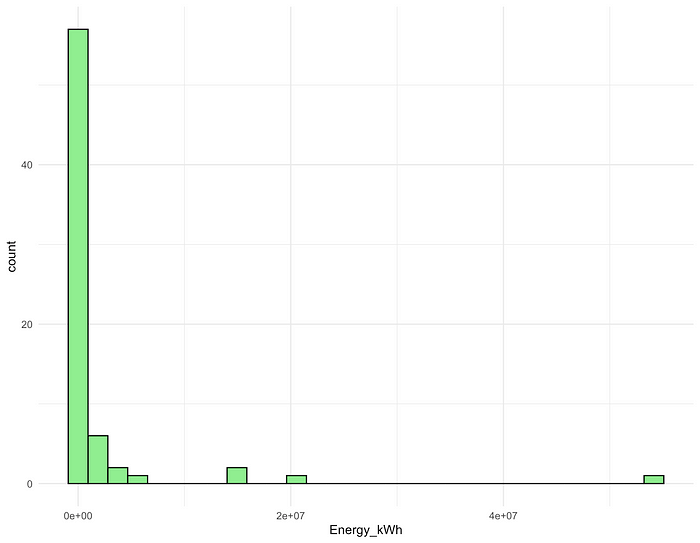
Bien que les distributions normales soient les plus couramment utilisées, de nombreuses données réelles ne sont malheureusement pas normales. Face à des données extrêmement biaisées, il est tentant pour nous d’utiliser les transformations de journal pour normaliser la distribution et stabiliser la variance. J’ai récemment travaillé sur un projet analysant la consommation d’énergie des modèles d’IA de formation, en utilisant les données de l’époque AI (1). Il n’y a pas de données officielles sur la consommation d’énergie de chaque modèle, donc je l’ai calculée en multipliant le tirage de puissance de chaque modèle avec son temps de formation. La nouvelle variable, l’énergie (en KWh), était très couverte à droite, ainsi que quelques valeurs aberrantes extrêmes et surdispersées (Fig. 1).

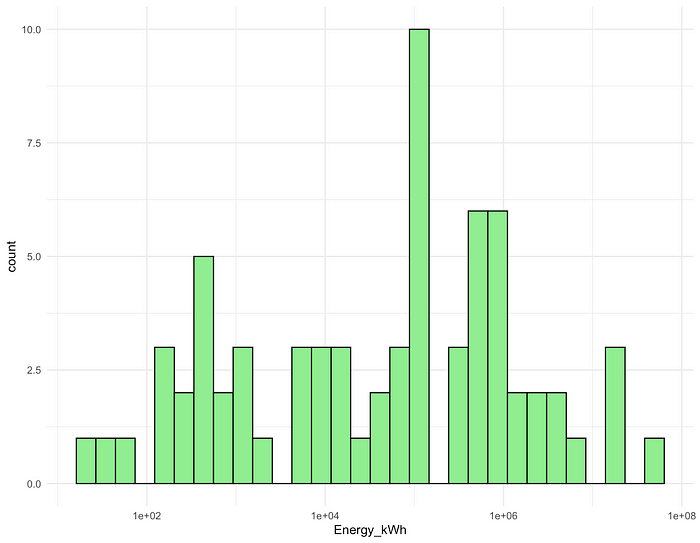
Pour aborder cette asymétrie et cette hétéroskédasticité, mon premier instinct a été d’appliquer une transformation de journal à la variable énergétique. La distribution du log (énergie) semblait beaucoup plus normale (Fig. 2), et un test de Shapiro-Wilk a confirmé la normalité limite (p ≈ 0,5)

Dilemme de modélisation: transformation du journal vs lien de journal

La visualisation avait l’air bien, mais quand je suis passé à la modélisation, j’ai fait face à un dilemme: devrais-je modéliser le Variable de réponse transformée en logarithme (journal (y) ~ x), ou devrais-je modéliser le Variable de réponse d’origine en utilisant un Fonction de liaison de journal (Y ~ x, link = « log »)? J’ai également envisagé deux distributions – les distributions gaussiennes (normales) et gamma – et combiné chaque distribution avec les deux approches logarithmiques. Cela m’a donné quatre modèles différents comme ci-dessous, tous ajustés à l’aide de modèles linéaires généralisés de R (GLM):

all_gaussian_log_link <- glm(Energy_kWh ~ Parameters +
Training_compute_FLOP +
Training_dataset_size +
Training_time_hour +
Hardware_quantity +
Training_hardware, 
family = gaussian(link = "log"), data = df)
all_gaussian_log_transform <- glm(log(Energy_kWh) ~ Parameters +
Training_compute_FLOP +
Training_dataset_size +
Training_time_hour +
Hardware_quantity +
Training_hardware, 
data = df)
all_gamma_log_link <- glm(Energy_kWh ~ Parameters +
Training_compute_FLOP +
Training_dataset_size +
Training_time_hour +
Hardware_quantity +
Training_hardware + 0, 
family = Gamma(link = "log"), data = df)
all_gamma_log_transform <- glm(log(Energy_kWh) ~ Parameters +
Training_compute_FLOP +
Training_dataset_size +
Training_time_hour +
Hardware_quantity +
Training_hardware + 0, 
family = Gamma(), data = df)

Comparaison du modèle: tracés AIC et diagnostique

J’ai comparé les quatre modèles à l’aide du critère d’information Akaike (AIC), qui est un estimateur de l’erreur de prédiction. En règle générale, plus l’AIC est faible, mieux le modèle s’adapte.

AIC(all_gaussian_log_link, all_gaussian_log_transform, all_gamma_log_link, all_gamma_log_transform)
df AIC
all_gaussian_log_link 25 2005.8263
all_gaussian_log_transform 25 311.5963
all_gamma_log_link 25 1780.8524
all_gamma_log_transform 25 352.5450

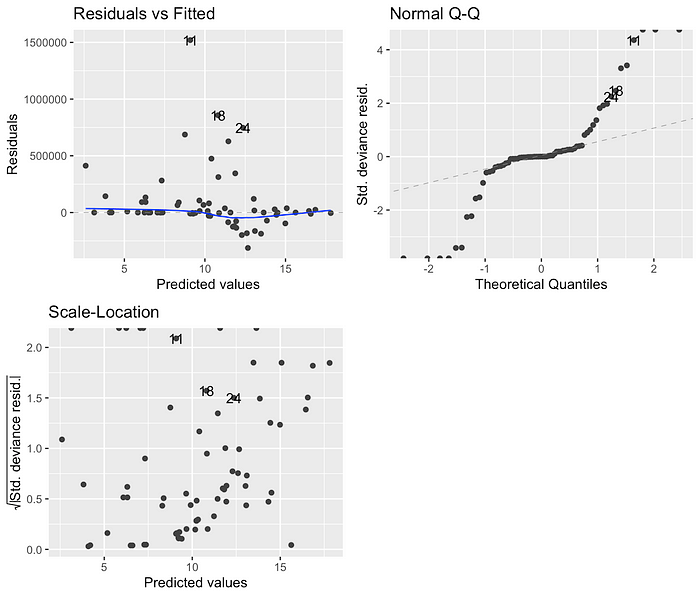
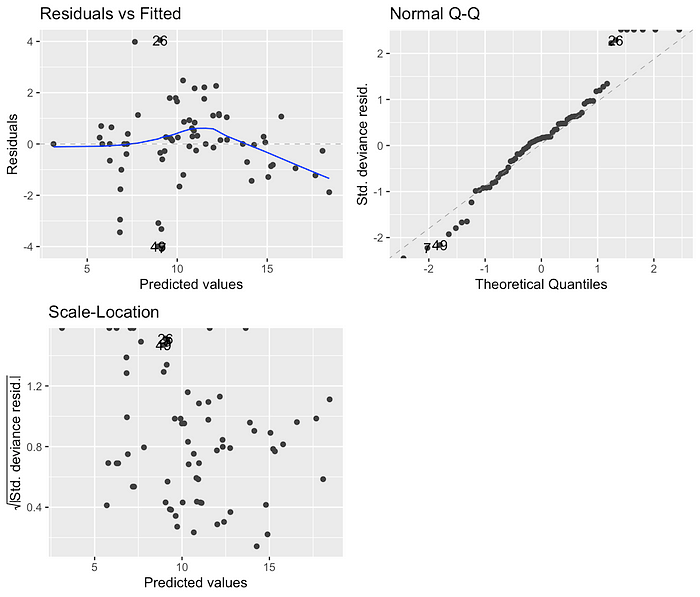
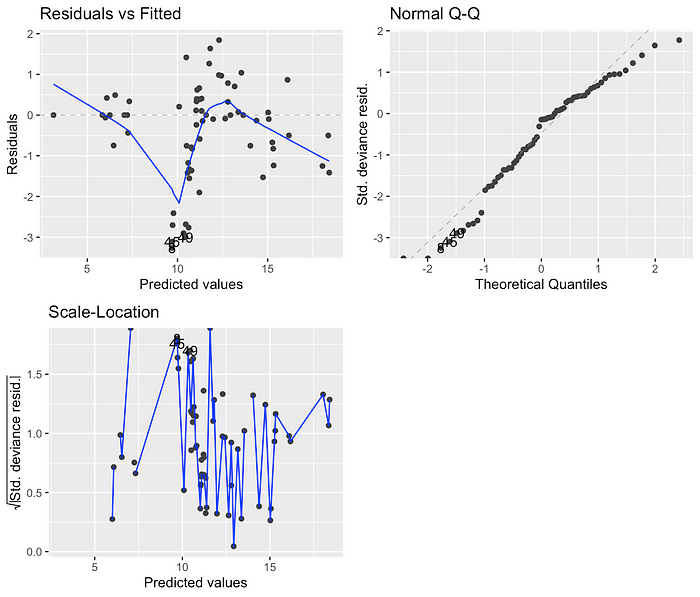
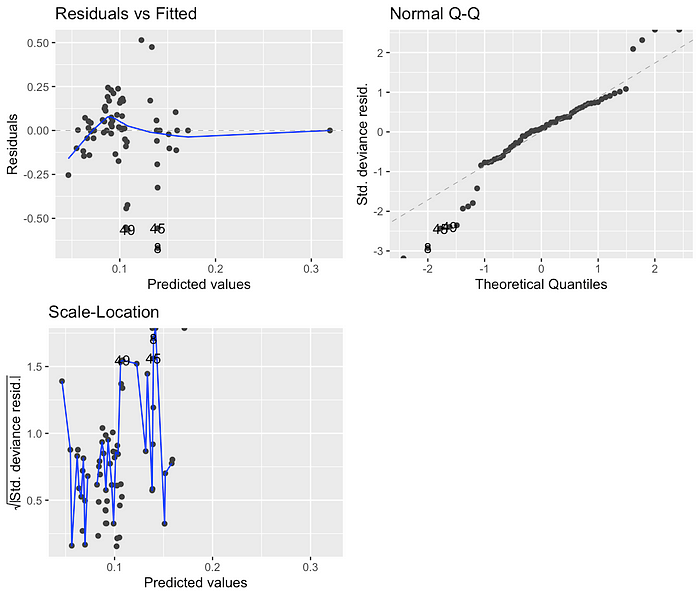
Parmi les quatre modèles, les modèles utilisant des résultats transformés en logarithme ont des valeurs AIC beaucoup plus faibles que celles utilisant des liens de journal. Étant donné que la différence d’AIC entre les modèles transformés en logarithme et logarithmique était substantiel (311 et 352 vs 1780 et 2005), j’ai également examiné les graphiques de diagnostic pour valider davantage que les modèles transformés par log s’adaptent mieux:

Sur la base des valeurs AIC et des tracés de diagnostic, j’ai décidé d’avancer avec le modèle gamma transformé en logarithme, car il avait la deuxième valeur AIC la plus bas et ses résidus vs ajustés semblent mieux que celui du modèle gaussien transformé en logarithme.

J’ai procédé à l’explorer quelles variables explicatives étaient utiles et quelles interactions peuvent avoir été significatives. Le modèle final que j’ai sélectionné était:

glm(formula = log(Energy_kWh) ~ Training_time_hour * Hardware_quantity + 
Training_hardware + 0, family = Gamma(), data = df)

Interprétation des coefficients

Cependant, lorsque j’ai commencé à interpréter les coefficients du modèle, quelque chose s’est senti éteint. Étant donné que seule la variable de réponse a été transformée en logarithme, les effets des prédicteurs sont multiplicatifs et nous devons exposer les coefficients pour les reconvertir à l’échelle d’origine. Une augmentation d’une unité en 𝓍 multiplie le résultat 𝓎 par exp (β), ou chaque unité supplémentaire en 𝓍 conduit à un changement (exp (β) – 1) × 100% en 𝓎 (2).

En regardant le tableau des résultats du modèle ci-dessous, nous avons Training_time_hour, hardware_quantity, et leur terme d’interaction Training_time_hour: hardware_quantity sont des variables continues, donc leurs coefficients représentent les pentes. En attendant, puisque j’ai spécifié +0 dans la formule du modèle, tous les niveaux de la catégorielle Training_hardware agit comme des interceptions, ce qui signifie que chaque type de matériel a agi comme l’interception β₀ lorsque sa variable fictive correspondante était active.

> glm(formula = log(Energy_kWh) ~ Training_time_hour * Hardware_quantity + 
Training_hardware + 0, family = Gamma(), data = df)
Coefficients:
Estimate Std. Error t value Pr(>|t|) 
Training_time_hour -1.587e-05 3.112e-06 -5.098 5.76e-06 ***
Hardware_quantity -5.121e-06 1.564e-06 -3.275 0.00196 ** 
Training_hardwareGoogle TPU v2 1.396e-01 2.297e-02 6.079 1.90e-07 ***
Training_hardwareGoogle TPU v3 1.106e-01 7.048e-03 15.696 < 2e-16 ***
Training_hardwareGoogle TPU v4 9.957e-02 7.939e-03 12.542 < 2e-16 ***
Training_hardwareHuawei Ascend 910 1.112e-01 1.862e-02 5.969 2.79e-07 ***
Training_hardwareNVIDIA A100 1.077e-01 6.993e-03 15.409 < 2e-16 ***
Training_hardwareNVIDIA A100 SXM4 40 GB 1.020e-01 1.072e-02 9.515 1.26e-12 ***
Training_hardwareNVIDIA A100 SXM4 80 GB 1.014e-01 1.018e-02 9.958 2.90e-13 ***
Training_hardwareNVIDIA GeForce GTX 285 3.202e-01 7.491e-02 4.275 9.03e-05 ***
Training_hardwareNVIDIA GeForce GTX TITAN X 1.601e-01 2.630e-02 6.088 1.84e-07 ***
Training_hardwareNVIDIA GTX Titan Black 1.498e-01 3.328e-02 4.501 4.31e-05 ***
Training_hardwareNVIDIA H100 SXM5 80GB 9.736e-02 9.840e-03 9.894 3.59e-13 ***
Training_hardwareNVIDIA P100 1.604e-01 1.922e-02 8.342 6.73e-11 ***
Training_hardwareNVIDIA Quadro P600 1.714e-01 3.756e-02 4.562 3.52e-05 ***
Training_hardwareNVIDIA Quadro RTX 4000 1.538e-01 3.263e-02 4.714 2.12e-05 ***
Training_hardwareNVIDIA Quadro RTX 5000 1.819e-01 4.021e-02 4.524 3.99e-05 ***
Training_hardwareNVIDIA Tesla K80 1.125e-01 1.608e-02 6.993 7.54e-09 ***
Training_hardwareNVIDIA Tesla V100 DGXS 32 GB 1.072e-01 1.353e-02 7.922 2.89e-10 ***
Training_hardwareNVIDIA Tesla V100S PCIe 32 GB 9.444e-02 2.030e-02 4.653 2.60e-05 ***
Training_hardwareNVIDIA V100 1.420e-01 1.201e-02 11.822 8.01e-16 ***
Training_time_hour:Hardware_quantity 2.296e-09 9.372e-10 2.450 0.01799 * 
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
(Dispersion parameter for Gamma family taken to be 0.05497984)
Null deviance: NaN on 70 degrees of freedom
Residual deviance: 3.0043 on 48 degrees of freedom
AIC: 345.39

Lors de la conversion des pentes en pourcentage de variation de variable de réponse, l’effet de chaque variable continue était presque nul, même légèrement négatif:

Toutes les interceptions ont également été converties à environ 1 kWh sur l’échelle d’origine. Les résultats n’avaient aucun sens car au moins une des pentes devrait croître avec l’énorme consommation d’énergie. Je me demandais si l’utilisation du modèle lié à journal avec les mêmes prédicteurs peut donner des résultats différents, donc j’adapte à nouveau le modèle:

glm(formula = Energy_kWh ~ Training_time_hour * Hardware_quantity + 
Training_hardware + 0, family = Gamma(link = "log"), data = df)
Coefficients:
Estimate Std. Error t value Pr(>|t|) 
Training_time_hour 1.818e-03 1.640e-04 11.088 7.74e-15 ***
Hardware_quantity 7.373e-04 1.008e-04 7.315 2.42e-09 ***
Training_hardwareGoogle TPU v2 7.136e+00 7.379e-01 9.670 7.51e-13 ***
Training_hardwareGoogle TPU v3 1.004e+01 3.156e-01 31.808 < 2e-16 ***
Training_hardwareGoogle TPU v4 1.014e+01 4.220e-01 24.035 < 2e-16 ***
Training_hardwareHuawei Ascend 910 9.231e+00 1.108e+00 8.331 6.98e-11 ***
Training_hardwareNVIDIA A100 1.028e+01 3.301e-01 31.144 < 2e-16 ***
Training_hardwareNVIDIA A100 SXM4 40 GB 1.057e+01 5.635e-01 18.761 < 2e-16 ***
Training_hardwareNVIDIA A100 SXM4 80 GB 1.093e+01 5.751e-01 19.005 < 2e-16 ***
Training_hardwareNVIDIA GeForce GTX 285 3.042e+00 1.043e+00 2.916 0.00538 ** 
Training_hardwareNVIDIA GeForce GTX TITAN X 6.322e+00 7.379e-01 8.568 3.09e-11 ***
Training_hardwareNVIDIA GTX Titan Black 6.135e+00 1.047e+00 5.862 4.07e-07 ***
Training_hardwareNVIDIA H100 SXM5 80GB 1.115e+01 6.614e-01 16.865 < 2e-16 ***
Training_hardwareNVIDIA P100 5.715e+00 6.864e-01 8.326 7.12e-11 ***
Training_hardwareNVIDIA Quadro P600 4.940e+00 1.050e+00 4.705 2.18e-05 ***
Training_hardwareNVIDIA Quadro RTX 4000 5.469e+00 1.055e+00 5.184 4.30e-06 ***
Training_hardwareNVIDIA Quadro RTX 5000 4.617e+00 1.049e+00 4.401 5.98e-05 ***
Training_hardwareNVIDIA Tesla K80 8.631e+00 7.587e-01 11.376 3.16e-15 ***
Training_hardwareNVIDIA Tesla V100 DGXS 32 GB 9.994e+00 6.920e-01 14.443 < 2e-16 ***
Training_hardwareNVIDIA Tesla V100S PCIe 32 GB 1.058e+01 1.047e+00 10.105 1.80e-13 ***
Training_hardwareNVIDIA V100 9.208e+00 3.998e-01 23.030 < 2e-16 ***
Training_time_hour:Hardware_quantity -2.651e-07 6.130e-08 -4.324 7.70e-05 ***
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
(Dispersion parameter for Gamma family taken to be 1.088522)
Null deviance: 2.7045e+08 on 70 degrees of freedom
Residual deviance: 1.0593e+02 on 48 degrees of freedom
AIC: 1775

Cette fois, Training_time et Hardware_quantity augmenterait la consommation d’énergie totale de 0,18% par heure supplémentaire et 0,07% par puce supplémentaire, respectivement. Pendant ce temps, leur interaction diminuerait la consommation d’énergie de 2 × 10⁵%. Ces résultats avaient plus de sens que Training_time peut atteindre jusqu’à 7000 heures et Hardware_quantity jusqu’à 16 000 unités.

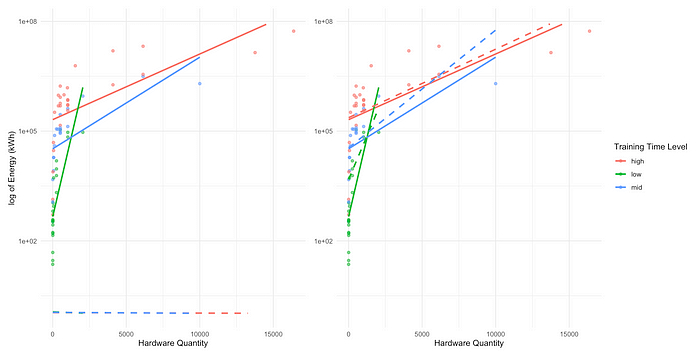
Pour mieux visualiser les différences, j’ai créé deux parcelles comparant les prédictions (représentées sous forme de lignes pointillées) à partir des deux modèles. Le panneau gauche a utilisé le modèle Gamma GLM transformé en journal, où les lignes en pointillés étaient presque plates et près de zéro, nulle part près des lignes pleines ajustées de données brutes. D’un autre côté, le panneau de droite a utilisé le modèle GAMMA GAMMA LIGNÉ, où les lignes en pointillés se sont alignées beaucoup plus étroitement avec les lignes ajustées réelles.

test_data <- df(, c("Training_time_hour", "Hardware_quantity", "Training_hardware"))
prediction_data <- df %>%
mutate(
pred_energy1 = exp(predict(glm3, newdata = test_data)),
pred_energy2 = predict(glm3_alt, newdata = test_data, type = "response"),
)
y_limits <- c(min(df$Energy_KWh, prediction_data$pred_energy1, prediction_data$pred_energy2),
max(df$Energy_KWh, prediction_data$pred_energy1, prediction_data$pred_energy2))
p1 <- ggplot(df, aes(x = Hardware_quantity, y = Energy_kWh, color = Training_time_group)) +
geom_point(alpha = 0.6) +
geom_smooth(method = "lm", se = FALSE) +
geom_smooth(data = prediction_data, aes(y = pred_energy1), method = "lm", se = FALSE, 
linetype = "dashed", size = 1) + 
scale_y_log10(limits = y_limits) +
labs(x="Hardware Quantity", y = "log of Energy (kWh)") +
theme_minimal() +
theme(legend.position = "none") 
p2 <- ggplot(df, aes(x = Hardware_quantity, y = Energy_kWh, color = Training_time_group)) +
geom_point(alpha = 0.6) +
geom_smooth(method = "lm", se = FALSE) +
geom_smooth(data = prediction_data, aes(y = pred_energy2), method = "lm", se = FALSE, 
linetype = "dashed", size = 1) + 
scale_y_log10(limits = y_limits) +
labs(x="Hardware Quantity", color = "Training Time Level") +
theme_minimal() +
theme(axis.title.y = element_blank()) 
p1 + p2

Pourquoi la transformation du journal échoue

Pour comprendre la raison pour laquelle le modèle transformé en logarithme ne peut pas capturer les effets sous-jacents en tant que log, parcourons ce qui se passe lorsque nous appliquons une transformation de journal à la variable de réponse:

Disons que y est égal à une fonction de x plus le terme d’erreur:

Lorsque nous appliquons un journal se transformant en Y, nous comprimons en fait à la fois f (x) et l’erreur:

Cela signifie que nous modélissons une toute nouvelle variable de réponse, log (y). Lorsque nous branchons notre propre fonction G (x) – dans mon cas g (x) = Training_time_hour * Hardware_quantity + Training_hardware – Il essaie de capturer les effets combinés à la fois du terme F (x) et du terme d’erreur « Shrunk ».

En revanche, lorsque nous utilisons un lien de journal, nous modélissons toujours le Y original, pas la version transformée. Au lieu de cela, le modèle exponentie notre propre fonction G (x) pour prédire Y.

Le modèle minimise ensuite la différence entre le Y réel et le Y. de cette façon prévu, les termes d’erreur restent intacts sur l’échelle d’origine:

Conclusion

La transformation du journal d’une variable n’est pas la même que l’utilisation d’un lien de journal, et il peut ne pas toujours donner des résultats fiables. Sous le capot, une transformation de journal modifie la variable elle-même et déforme à la fois la variation et le bruit. Comprendre cette subtile différence mathématique derrière vos modèles est tout aussi important que d’essayer de trouver le modèle le mieux adapté.

(1) Epoch Ai. Données sur les modèles d’IA notables. Récupéré de https://epoch.ai/data/notable-ai-models

(2) Bibliothèque de l’Université de Virginie. Interpréter les transformations de journal dans un modèle linéaire. Récupéré de https://library.virginia.edu/data/articles/interpreting-log-transformations-in-a-linear-model

Publié via Vers l’IA