Le mathématicien trouve une solution à l’un des plus anciens problèmes de l’algèbre: ScienceAtt

Résoudre l’un des plus anciens problèmes d’algèbre n’est pas une mauvaise prétention à la gloire, et c’est une affirmation que Norman Wildberger peut maintenant faire: le mathématicien a résolu ce qui est connu sous le nom de degré supérieur équations polynomialesqui est déroutant des experts depuis près de 200 ans.

Wildberger, de l’Université de Nouvelle-Galles du Sud (UNSW) en Australie, a travaillé avec l’informaticien Dean Rubine sur un journal qui détaille comment ces calculs complexes pourrait être élaboré.

« Il s’agit d’une révision spectaculaire d’un chapitre de base de l’algèbre »,  » dit Wildberger. « Notre solution rouvre un livre précédemment fermé en histoire des mathématiques. »

Comme vous pouvez vous y attendre, comprendre comment cela fonctionne n’est pas facile pour les génies non algèses parmi nous. Essentiellement, les polynômes sont des équations qui incluent des variables soulevées aux pouvoirs non négatifs (par exemple x³). Lorsque ces pouvoirs sont cinq ou plus, c’est un polynôme de degré plus élevé.

Les mathématiciens ont compris comment résoudre des versions à basse durée, mais on pensait que le calcul correct des degrés plus élevés était impossible. Avant cette nouvelle recherche, nous comptons sur des approximations.

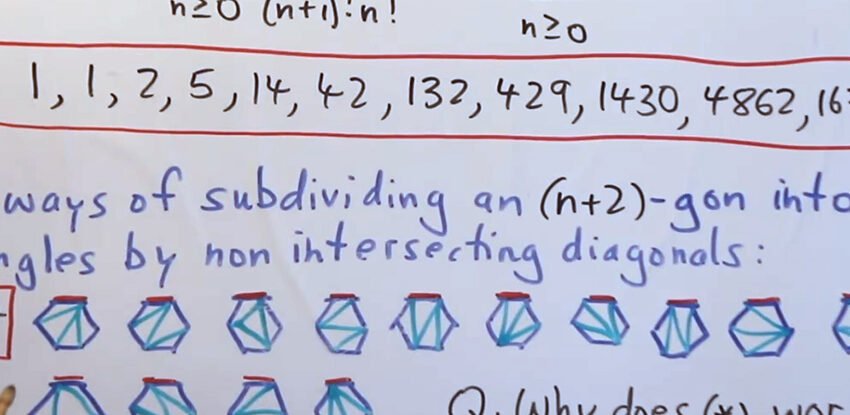
Wildberger et Rubine ont adopté une nouvelle approche du problème, qui est basé sur Nombres catalans. Ces nombres sont utilisés dans le comptage et les arrangements avancés des nombres, y compris le comptage du nombre de façons de polygones peuvent être subdivisés en triangles.

En étendant l’idée des nombres catalans, les chercheurs ont pu démontrer qu’ils pourraient être utilisés comme base pour résoudre les équations polynomiales de tout degré. Une partie de la méthode intelligente impliquait d’étendre le nombre de polygones à d’autres formes en plus des triangles.

C’est un Départ de la méthode traditionnelle de l’utilisation expressions radicales (comme les racines carrées et les racines du cube) pour résoudre des équations comme celle-ci, en comptant plutôt sur combinatoire – Compter les chiffres, fondamentalement, mais de plus en plus avancés.

« Les nombres catalans sont comprités comme étant intimement connectés à l’équation quadratique, » dit Wildberger.

« Notre innovation réside dans l’idée que si nous voulons résoudre des équations plus élevées, nous devons rechercher des analogues plus élevés des nombres catalans. »

https://www.youtube.com/watch?v=oihd3zdddce frameborder = « 0 ″ allow = » accéléromètre; AutoPlay; Clipborat-écriture; médias cryptés; gyroscope; image dans une image; web-share « RefraierPolicy = » strict-original-when-cross-origin « allowerlScreen>

Les chercheurs ont mis leur nouvelle algèbre contre certaines équations polynomiales bien connues du passé, y compris une célèbre équation cubique étudiée par John Wallis. Les nombres ont vérifié, validant les nouveaux travaux.

Wildberger et Rubine ne se sont pas arrêtés là. Ils ont également découvert une nouvelle structure mathématique appelée Geode, qui se lie aux nombres catalan et semble agir comme une base pour eux. Cette géode pourrait former la base de nombreuses études et découvertes futures, selon les chercheurs.

Comme l’approche adoptée ici est si différente de ce qui s’est déroulé avant, il y a le potentiel de repenser de nombreuses idées clés sur lesquelles les mathématiciens s’appuyaient depuis longtemps pour les algorithmes informatiques, la façon dont les données sont structurées et théorie des jeux. Il pourrait même avoir des applications en biologie – pour compter Pliage de molécule d’ARNPar exemple.

« Il s’agit d’un calcul de base pour une grande partie des mathématiques appliquées, c’est donc une opportunité d’améliorer les algorithmes dans un large éventail de domaines »  » dit Wildberger.

La recherche a été publiée dans Le mensuel mathématique américain.